Annexe - Le support mathématique sous jacent

Marche aléatoire

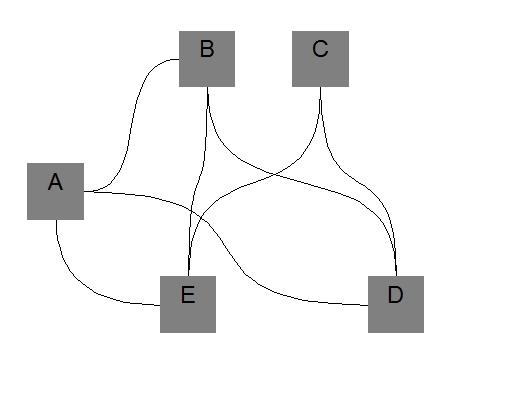
Considérons un graphe non orienté G = (V;E) qui possède n = V sommets et n = E arêtes.

Notre graphe est connexe (il existe toujours un chemin pour aller vers les sommets).

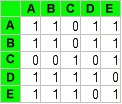
Ce graphe peut être représenté par une matrice d’adjacence A avec Aij = 1 si les sommets i et j sont reliés par une arête et Aij = 0 dans le cas contraire. Comme notre graphe est pondéré, les 1 sont remplacés par les valeurs de pondération comprise dans l’intervalle [0; 1].

Transformation d’un graphe en matrice d’adjacence

Le degré d’un sommet est la somme des arêtes qui le rejoignent donc pour un sommet i on a:

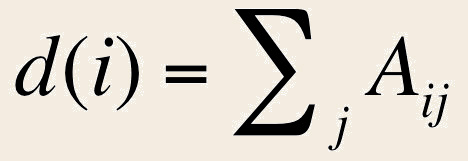avec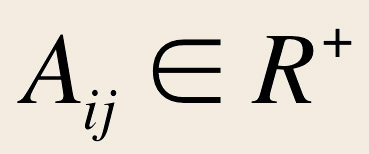

La marche aléatoire utilisée dans ce modèle est un processus de diffusion dans le graphe. À chaque instant, un marcheur est localisé sur un sommet du graphe et se déplace au temps discret suivant vers un sommet choisi aléatoirement et uniformément parmi les sommets voisins. La suite des sommets visités correspond bien à une marche aléatoire, et la probabilité de transition du sommet i au sommet j est, à chaque étape, calculée par l’équation suivante:

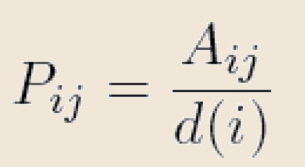Ceci donne une matrice de transition P correspondant à cette marche aléatoire. La matrice de transition caractérise entièrement la marche (le processus aléatoire), puisqu’elle spécifie l’espace dans lequel elle s’effectue (le graphe), les sauts possibles (les connexions du graphe) et les probabilités des sauts. C’est finalement la description mathématique du territoire traité et de la manière dont il est utilisé en fonction des hypothèses que nous nous sommes fixées.

Une matrice de transition doit posséder deux propriétés. Ses coefficients doivent  être des réels de [0, 1] (Il s’agit de probabilités), et la somme des coefficients de n’importe quelle ligne doit valoir 1.

Le mécanisme de diffusion se fait de la façon suivante. Étant donné une probabilité de position pt du marcheur à l'instant t, la probabilité de le trouver sur le sommet j à l'instant suivant est donnée par l’équation:

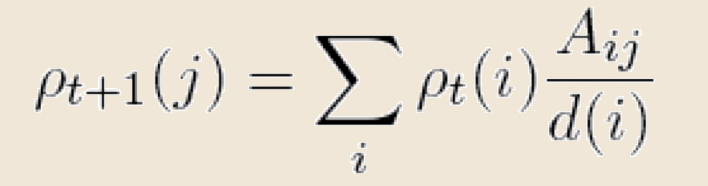Ce mécanisme permet de calculer une probabilité d’aller du sommet i au sommet j en t étapes. Le choix d’arrêter le processus au temps t + n permet de calculer la portée de diffusion d’un sommet dans l’ensemble comme le montre l’exemple pédagogique ci-dessous.

Calcul d’une probabilité d’atteinte du nœud j à partir du nœud i en trois itérations. (source de l’image: Pons P)

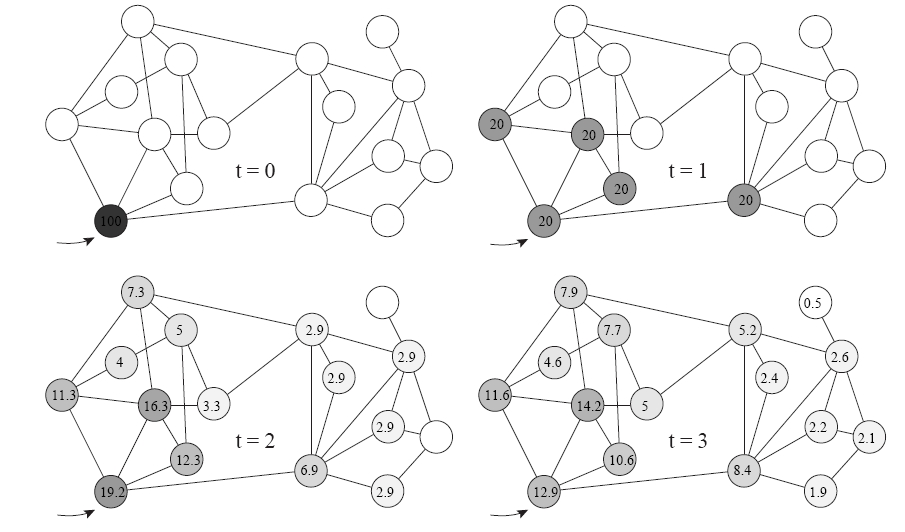Betweenness Centrality

Il s’agit d’un indicateur qui permet de classer les sites en fonction du nombre de fois qu’ils sont empruntés dans un contexte de chemin (Wasserman, Faust 1994). C'est-à-dire le nombre de fois qu’un site X est obligatoirement emprunté entre un site A et un site B. Les sites avec une forte valeur de centralité sont des sites qui «contrôlent» la diffusion globale dans le graphe. Ils sont donc plus centraux que les autres.

Cet indicateur est obtenu avec l’équation suivante:

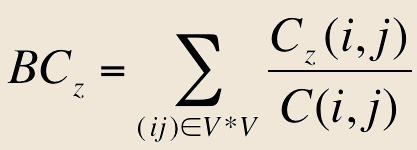Avec z = un sommet quelconque,

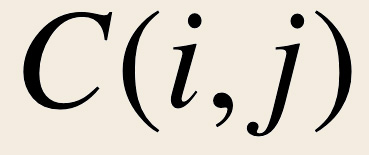et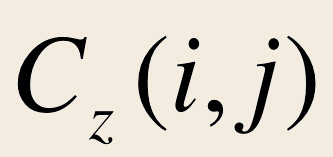

Degré

Le degré d’un sommet est la somme des arêtes auxquelles il appartient, donc pour un sommet i on a:

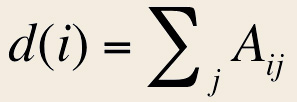avec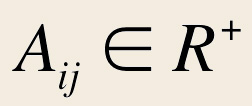