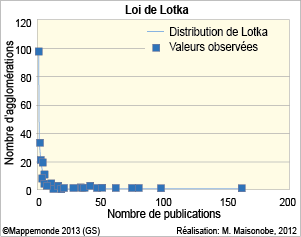
| Encadré 1. La loi Lotka | |
Tout comme les lois de Pareto et Zipf (1935), la loi de Lotka (1926) est une de loi de puissance. Elle établit que le nombre d’auteurs publiant i articles est inversement proportionnel au carré d’articles publiés. Donc, ce nombre est égal à: ni = n1/i2, i = 1, 2, 3... imax Où n1 est le nombre de scientifiques ayant écrit un article et imax le nombre maximum d’articles écrits par un auteur (Polanco, 1995; Solla-Price, 1963). Cette loi traduit le fait que l’essentiel de la production est le fait d’une petite poignée de publiants. Les scientomètres ont largement recours à cette loi pour expliquer ou comparer les distributions très asymétriques auxquelles ils ont à faire. Cependant, l’exposant 2 retenu par Lotka ne se retrouve pas souvent dans la réalité. Il implique qu’environ 60% des auteurs d’un échantillon donné ne publient qu’un seul article. Les pratiques de publications ayant évolué: imax tend à être plus grand et n1 plus petit. Pour notre cas d’étude, on montre que la relation existe, y compris si l’on prend comme variable à expliquer la productivité des agglomérations et non celle des auteurs. Ainsi, 98 agglomérations (40%) n’ont publié qu’un seul article. Par conséquent, l’exposant le mieux adapté pour décrire la relation est de 1,5; ce que confirment par ailleurs les résultats du test d’adéquation de Kolmogorov-Smirnov. On obtient la fonction suivante: Y=b/ Xa où b=98 et a=1,5 | Ainsi, 5% des agglomérations sont responsables de 80% de la production et ce ratio est proportionnel aux agglomérations n’ayant publié qu’un seul article.
|