Découpage hiérarchique du réseau

Nous avons envisagé d’appliquer au réseau une méthodologie élaborée par D. Auber et al. en 2003, qui permet de hiérarchiser le réseau en fonction des densités de connexion entre des groupes de nœuds. Les algorithmes qu’ils ont mis au point sur des graphes non-valués ont été adaptés pour les graphes valués.

Éclatement de la topologie du réseau

La technique développée par Auber et al. procède par filtrage des arêtes d’un graphe connexe afin de le décomposer en sous-graphes. Ces sous-graphes correspondent simplement aux composantes les plus connexes du graphe, mises en évidence en supprimant les arêtes qui participent le moins aux connectivités locales. La procédure peut être répétée sur chacun des sous-graphes et fait ainsi apparaître une hiérarchie de sous-graphes emboîtés.

Filtrage des arêtes

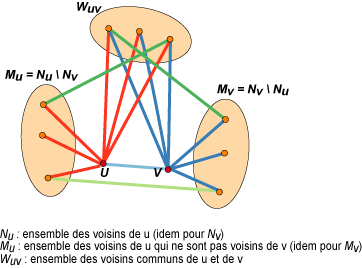
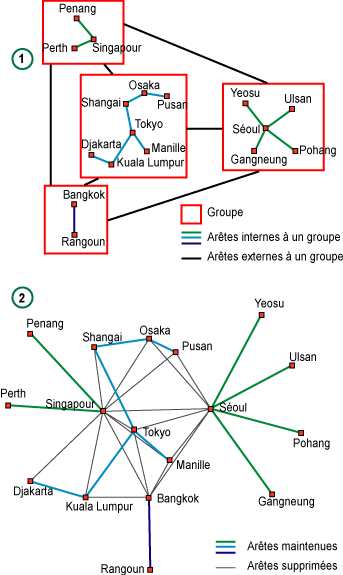
I. Méthode de filtrage des arêtes	II. Exemples de filtrage des arêtes

Un filtrage est effectué sur la base d’une valeur associée à chaque arête. La valeur associée à une arête reflète la cohésion qu’elle apporte à son voisinage. L’indice de cohésion d’une arête est en quelque sorte une généralisation de l’indice de clustering d’un sommet introduit par Watts et Strogatz dans la théorie des réseaux «petits mondes» (small world networks) (Watts, Strogatz, 1998; Watts, 1999). Cet indice de cohésion s’obtient en calculant le ratio entre le nombre de liens effectifs entre les voisins des sommets incidents à l’arête, et le nombre maximal de liens qui pourraient être observés (fig. I). Parmi les voisins des deux sommets incidents à l’arête, il est nécessaire de distinguer leurs voisins communs (l’ensemble Wuv sur la figure) et ceux qui ne sont voisins que de l’un des deux sommets. L’importance du nombre de voisins communs par rapport à ceux qui ne sont pas communs va déterminer si l’arête est maintenue ou non. Par exemple, sur la figure II, seules les arêtes dont les nœuds ont plus (ou autant) de voisins communs que de voisins non communs sont maintenus (en rouge).

Prise en compte du trafic

Pour obtenir un découpage pertinent du réseau formé des flux aériens de passagers, il nous a fallu adapter la méthodologie de Auber et al., en prenant en compte le poids des arêtes du graphe qui représentent le trafic aérien. En effet, cette méthode repose sur la topologie du réseau étudié, misant entièrement sur ses propriétés «petits mondes» et laissant de côté l’importance des échanges.

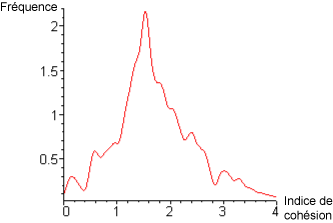
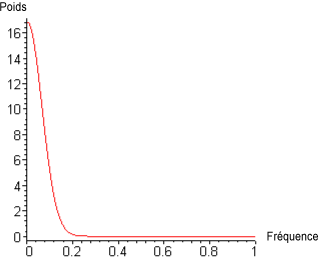
III. Distribution de l'indice de cohésion des arêtes	IV. Distribution des poids des arêtes (trafics aériens)

La distribution de ces échanges, soit le poids des arêtes du graphe, suit ici une distribution «scalefree» ce qui rend compte de la forte hiérarchisation du réseau aérien mondial (fig. IV). Afin de tenir compte de ces poids, nous avons soumis à l’examen du filtrage les valeurs obtenues en multipliant l’indice de cohésion des arêtes par leurs poids respectifs. Ainsi, la prise en compte des poids produit un découpage du réseau plus pertinent.