N°112

CARTOD/MAPOD : Visualiser la demande locale de transport

Objectifs et contextes de développement

L’objectif de l’application CARTOD est de permettre la géovisualisation de l’ensemble de l’information présente dans une matrice de flux sous la forme d’un graphe spatialisé et cela, sans opérer de sélection a priori des valeurs à représenter.

La représentation des flux pose, en effet, un problème majeur de lisibilité lorsque la matrice est dense. Sachant que le nombre d’arêtes est fonction du nombre N de lieux d’origine et de destination, les N(N-1) figurés qui les représentent se traduisent sur la figure par un chevauchement trop important: c’est l’effet spaghetti (Breukelman et al., 2009). Ce problème général étant aussi de nature topologique, puisque les lieux sont nécessairement localisés, deux solutions sont envisageables en plus de l’utilisation d’une sémiologie adaptée. La première vise à agir sur la localisation des arêtes et la seconde sur celle des nœuds, soit respectivement sur les flux et sur les lieux.

L’application CARTOD est ainsi fondée sur un mode de représentation inédit qui s’inspire d’une part, du diagramme en cordes (chord diagram, Stoica et al., 2001) et de l’autre, sur une méthode de déformation des arêtes et des sommets (Holten, 2006); tous deux assurent la lisibilité de la figure et la conservation des motifs des flux à l’échelle concernée.

CARTOD a été développée dans le cadre du Projet Belgrand-GEBD: Grand Équipement Bases de Données pour l’ingénierie des données sur la ville, en lien avec le groupe FMR (flux matrices réseaux). La réalisation informatique s’appuie sur le logiciel open source de visualisation des flux Jflowmap (Boyandin et al., 2010), que nous avons étendu en intégrant une méthode de classification fonctionnelle par les flux, ainsi qu’une procédure de transformation des régions en cercles équivalents.

Présentation de l’application

1. Cartographie directe des flux domicile – travail à l’échelle de la France (version 1)

La demande de transport s’exprime généralement sous la forme d’une matrice de flux Origine/Destination (OD) sur un maillage territorial. Les valeurs qu’elle contient résultent de la comptabilisation du nombre d’individus qui se sont déplacés depuis une maille d’origine vers une maille de destination, pendant une période de temps donnée. L’information obtenue est de nature topologique: les flux associés à cette matrice sont agrégés; ils ne sont pas localisés précisément. Autrement dit, l’itinéraire que les individus ont emprunté entre les mailles n’est pas connu, seuls leurs lieux d’origine et de destination sont renseignés de manière imprécise car ils sont assimilés au centre de la maille.

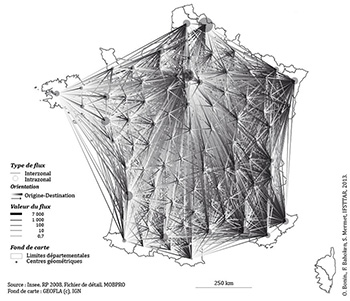
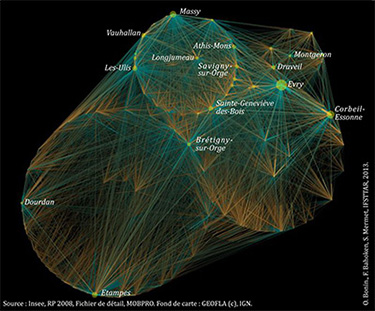
La géovisualisation d’une matrice OD pose des problèmes spécifiques liés à la composante spatiale, à la quantité et à la valeur des arêtes. Du fait de contraintes physiques de distance et de temps, une matrice OD à courte distance aura une structure spatiale très différente d’une matrice OD à longue distance. À longue distance, les flux observés coïncident avec des moyens de transport rapides tandis qu’à courte distance, ils peuvent être répartis dans toutes les directions. Ainsi, leur représentation naïve — par exemple, sous la forme de cartes de flux classiques qui associent à tout couple d’OD une arête d’épaisseur proportionnelle à la valeur du flux — produit des cartes à peu près lisibles sur longue distance, à petite échelle, mais illisibles pour les moyennes et courtes distances (fig. 1).

Sur la figure 1, les arêtes sont représentées par des bandes affectées d’une double coloration, afin de ne pas recourir au modèle graphique de la flèche qui pose nombre de contraintes graphiques spécifiques. Une première manière de l’améliorer consiste à utiliser une sémiologie graphique adaptée à la cartographie de flux réalisée sur un support-écran, telle qu’elle est mise en œuvre dans le champ de la visualisation des données. Elle agit sur la variable visuelle couleur au niveau global de la perception d’ensemble, ainsi qu’au niveau local de la représentation des figurés.

2. Cartographie directe de flux domicile – travail à l’échelle de la France (version 2)

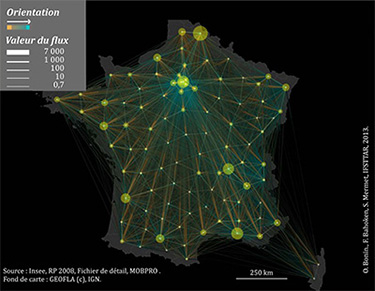
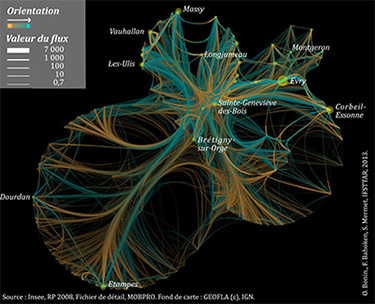
Sur le plan global, nous avons fait le choix d’utiliser un fond noir qui facilite la visualisation de la masse de petits flux diffus qui n’étaient pas perceptibles autrement, les plus gros flux étant par ailleurs rendus plus visuellement saillants. Au niveau local, l’utilisation d’un gradient translucide de couleurs opposées, depuis les lieux d’origine vers les lieux de destination, représenté respectivement par des teintes chaudes, en orange, vers les teintes froides, en bleu, permet de représenter efficacement l’orientation des flux, tout en illustrant l’émissivité et la réceptivité des lieux (fig. 2).

Le recours à des couleurs luminescentes rend par ailleurs, de notre point de vue, la carte plus efficace; elle autorise aussi plusieurs niveaux de lecture du système de mobilités représenté.

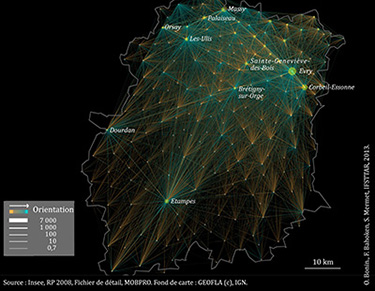
Cependant, malgré son efficacité, cette amélioration d’ordre sémiologique est insuffisante dans le contexte de la courte distance qui pose des problèmes spécifiques de lisibilité. Pour l’illustrer, nous avons généré une matrice de flux domicile – travail du département de l’Essonne (91), à partir du fichier de détail des mobilités professionnelles des individus (MOBPRO) issu de l’exploitation complémentaire du recensement réalisé par l’Insee pour l’année 2008. Cet ensemble est composé de 196 communes, ce qui porte à 38 220 le nombre potentiel d’arêtes à représenter sur la carte. La densité de la matrice étant de 22%, 8 689 figurés sont représentés sur la figure 3.

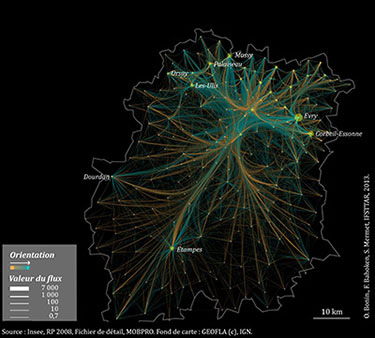
3. Cartographie directe de flux domicile – travail de l’Essonne 4. Cartographie directe d’une sélection de flux domicile – travail de l’Essonne

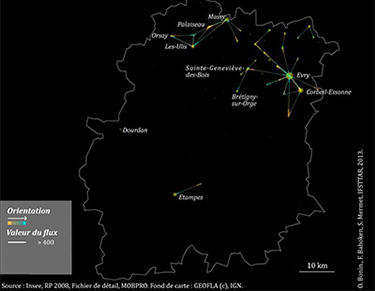La solution paramétrique qui consiste à sélectionner certains flux, pour ne conserver que ceux qui présentent les valeurs les plus importantes, repose sur une valeur de seuil nécessairement arbitraire. Elle produit des cartes certes intéressantes mais qui font disparaître la structure diffuse des OD ainsi que les différences d’attractivité des lieux (fig. 4).

Plutôt que de sélectionner les valeurs de flux à cartographier, nous proposons d’agir sur l’espace. La matrice OD étant représentée par un graphe spatialisé dont les arêtes sont représentées par une sémiologie particulière, nous pouvons, en effet, intervenir à la fois sur le tracé des arêtes et sur la position des nœuds. Nous suggérons ainsi de conserver l’ensemble de l’information disponible dans la matrice, mais de modifier la représentation euclidienne de l’espace selon deux modalités. La première porte sur la déformation des arêtes et la seconde sur la position des nœuds.

La déformation des arêtes

La première modalité de modification de la représentation que nous proposons porte sur la déformation des arêtes qui ne rejoignent plus en ligne droite les couples d’OD mais sont déformées de manière à fusionner visuellement. Le principe sous-jacent à ce mode de représentation est celui de l’agrégation graphique hiérarchique des arêtes proposée par Holten (2006), sous la dénomination d’edge bundling.

Il s’agit d’une méthode de visualisation des données relationnelles développée en informatique. Elle consiste à fusionner visuellement les arêtes en respectant la topologie des lieux et cela, en fonction d’une force d’attraction des nœuds et des arêtes. Elle autorise donc une action sur trois composantes spatiales:

5. Fusion graphique des flux domicile – travail de l’Essonne

Le regroupement des arêtes des flux de l’Essonne est représenté sur la figure 5. La méthode permet d’augmenter la lisibilité de la carte tout en conservant, en renforçant les motifs généraux des mobilités à l’échelle de la zone étudiée. Elle met en évidence comme des couloirs préférentiels d’écoulement qui correspondent à l’orientation générale des flux qui présentent les valeurs les plus importantes (fig. 5).

Notre troisième proposition conserve cette orientation générale des flux ainsi que la proximité des lieux, tout en modifiant leur position dans l’espace.

La transformation de la position des lieux

La deuxième modalité de modification de la représentation que nous proposons porte sur la localisation des lieux. Elle permet d’obtenir une information complémentaire à celle présentée sur la figure 5.

L’information spatialisée qui porte sur des flux étant de nature topologique, il est possible de modifier la position absolue des lieux sans nuire à la lisibilité de la carte, à condition de conserver des propriétés relatives telles que les relations cardinales et les ordres de grandeur de distances entre les lieux. Il s’agit d’une schématisation, souvent effectuée à la main que nous proposons d’automatiser et de rendre interactive.

Pour cela, nous sommes repartis du mode de représentation en diagramme par cordes, une variante du diagramme circulaire développé au MIT pour visualiser les structures relationnelles de type pair à pair (Stoica et al., 2001), pour proposer une nouvelle vision de l’espace des flux. L’idée sous-jacente est celle d’une représentation équivalente au modèle euclidien qui respecte les directions cardinales des flux, la proximité des lieux ainsi que la structure spatiale de type centre-périphérie des aires fonctionnelles de l’espace étudié. Elle prend la forme d’une série de cercles emboîtés dont les périmètres accueillent les lieux qui y sont projetés. La position centrale ou périphérique des lieux correspond à leur position dans l’aire fonctionnelle dont il est question. Ainsi, les lieux situés sur les cercles internes ont une position centrale dans la région fonctionnelle dégagée par la procédure de classification associée et inversement, pour les lieux projetés sur le cercle externe.

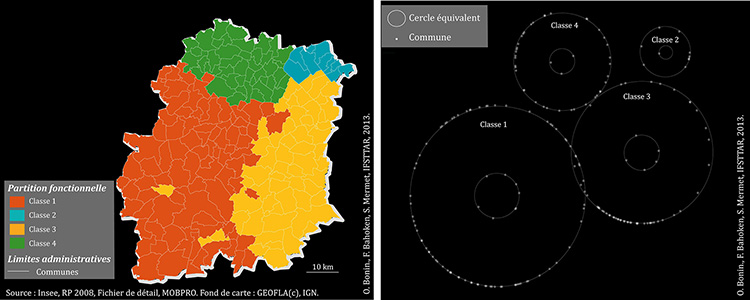
6. Représentation de la localisation des communes de l’Essonne projetées sur des classes fonctionnelles de cercles équivalents

Les nouvelles positions des flux OD sont dès lors obtenues en deux étapes. Nous réalisons d’abord une classification fonctionnelle (Bahoken, Costa, 2011) des flux, afin de partitionner l’espace en sous-régions homogènes qui ont leur propre structure interne, puis nous décidons du nombre de classes à représenter. Nous schématisons ensuite les sous-régions fonctionnelles obtenues en projetant les communes concernées sur les doubles cercles équivalents pour conserver la structure centre-périphérie (fig. 6 et 7).

7. Projection des flux domicile – travail de l’Essonne sur les classes de cercles équivalents

Nous représentons ensuite, à l’aide de la même technique de regroupement des arêtes, l’ensemble des flux entre les communes (fig. 8). Ce nouveau mode de visualisation fait apparaître d’une part, le fonctionnement interne des régions, les liens entre les régions ainsi que les zones d’interfaces; et d’autre part, l’attractivité des lieux.

Cette acceptation circulaire de l’espace des flux est innovante, elle diffère aussi de propositions fondées sur le diagramme circulaire. En cartographie, la question de la modification de la position des lieux, lorsque leur implantation spatiale est ponctuelle, n’est pas, à notre connaissance, questionnée. La position des lieux est, en effet, toujours supposée absolue et, lorsqu’elle ne l’est pas, les lieux sont appréhendés en implantation surfacique. Dans le cas de l’anamorphose scalaire (Cauvin, 1998), la transformation de la position des lieux est réalisée sur des polygones et pas sur des points. Elle est toujours associée à une déformation morphologique — dont l’ampleur est une fonction de la valeur prise par un indicateur (la population par exemple) — qui entraîne une modification de la position du barycentre de la commune. Dans le cas des anamorphoses vectorielles (Tobler, 1986), la transformation de la position des lieux résulte de celle des couples de lieux en interaction; elle porte sur la valeur du flux, par conséquent de l’arête, ce qui n’est pas notre cas. De la même façon, notre proposition diffère du «kriskogram»proposé par Xiao et Chun (2009) qui est fondé sur des demi-arcs de cercles et du diagramme circulaire classique qui ne respecte ni l’orientation ni la proximité des lieux. Ainsi, hormis la localisation en x et y des lieux, les autres composantes liées aux flux sont maintenues: il s’agit du niveau de résolution spatiale (l’échelle), de l’orientation (α°), du nombre N de lieux, de la quantité de figurés qui illustrent les flux et leur valeur.

8. Fusion graphique des flux domicile – travail de l’Essonne projetés sur des classes de cercles équivalents

L’application proposée est autonome, dynamique et interactive, dans la mesure où l’on peut faire varier le nombre de sous-régions fonctionnelles et la manière dont les arêtes s’attirent mutuellement.

Bibliographie

BAHOKEN F., COSTA N. (2011). «Functional Regions based on Intramax procedures». In GRASLAND C., VAN HAMME G., dir., Statistical Toolbox for flows and network analysis. Deliverable D.5.1. EuroBroadMap.Vision of Europe in the World. Small or medium scale focused project FP7-SSH-2007-1, p. 11-20. (consulter)

BOYANDIN I., BERTINI E., LALANNE D. (2010). «Using Flow Maps to Explore Migrations Over Time». Proceedings of Geospatial Visual Analytics Worskshop in conjunction with the 13th AGILE International Conference on Geographic Information Science (GeoVa). Portugal : Guimaraes, 4 p. (consulter)

BREUKELMAN J., BRINK G., DE JONG T., FLOOR H. (2009). Selecting Flow Data, Manual. Flowmap software v.3. Utrecht: Utrecht University, Sciences the Netherlands, Faculty of Geographical, p. 42-44.

CAUVIN C. (1998). «Des transformations cartographiques». Mappemonde, n° 49, 4 p.

HOLTEN D. (2006). «Hierarchical edge bundles: Visualization of adjacency relations in hierarchical data». Proceedings of the IEEE Transactions on Visualization and Computer Graphics, vol. 12, n° 5, p. 741-748.

STOICA I., MORRIS R., KARGER D., FRANS KAASHOEK M., BALAKRISHNAN H. (2001). «Chord: A Scalable Peertopeer Lookup Service for Internet Applications». Proceedings of the SIGCOMM’01 Conference, August 27-31, 2001, San Diego, California, USA, 12 p.

TOBLER W. (1986). «Bidimensional Regression». Geographical Analysis, vol. 26, n° 3, p. 187-212.

XIAO N., CHUN Y. (2009). Visualizing migration flows using kriskograms. Cartography and Geographic Information Science, vol. 36, n° 2, p. 183-191.

Projet réalisé dans le cadre d'un partenariat entre l'ENSCI (Atelier Informe, sous la direction de Stéphane Villard) et le musée du quai Branly (Direction des Publics) autour des nouvelles formes de médiation culturelle.