Logiciel open source pour la création automatique de villes en 3D à partir de données SIG standard
Introduction
De nombreux SIG propriétaires proposent des conversions de données SIG en 3D tels que ArcGIS avec son module 3D analyst (Kennedy, Squividant, 2004) ou MapInfo. La visualisation de villes en 3D a été popularisée avec l'arrivée de Google Earth sur nos écrans. Le plugin permettant d’extruder les bâtiments est souvent utilisé pour mieux se localiser dans la ville affichée. Entre les outils proposés par ESRI ou Pitney Bowes Softwares et ceux de Google se trouve un large fossé. Nous avons d’un côté des SIG complets, dédiés au monde de la géomatique et nécessitant une connaissance dans ce domaine et, de l’autre côté, un outil très simple d’utilisation, mais n’offrant pas ou peu d’interaction sur la donnée et sur l’environnement virtuel. Mon travail de thèse se base sur ce fait et apporte une solution intermédiaire qui est de construire des villes en 3D de manière automatique, tout en ayant la main sur ce que l’on voit. Ce travail est une base sur laquelle on peut imbriquer des modules de simulation. Un module de circulation routière est en cours de construction dans ce but. Nous présenterons dans cet article la mise en place de la conversion de données SIG en 3D ainsi que certains outils de visualisation développés jusqu’à aujourd’hui.
De la donnée 2.5D vers la 3D
Cas des bâtiments
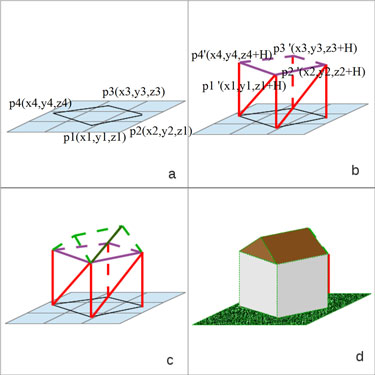
| 1. Extrusion d'une donnée SIG 2.5D avec ajout d'un toit |
Certaines données SIG vectorielles sont considérées comme données 2,5D. C'est le cas quand un attribut lié à l'objet (de type point, ligne, ou polygone) correspond à une élévation ou à une hauteur. Par exemple, la donnée de bâti issue de la BD TOPO de l'IGN contient un attribut hauteur dans lequel se trouve, pour chaque bâtiment, sa hauteur par rapport à sa base. Nous allons utiliser cet attribut pour créer notre objet 3D. La figure 1 illustre le principe de l'extrusion de la donnée bâti.
La première étape (a) est de connaître la position (X,Y,Z) de chaque sommet de notre objet 2D. Les coordonnées (X,Y) sont données directement par le SIG, nous le rattachons ensuite à un Z, correspondant à la topographie sous-jacente. Ensuite (b), un projeté de chaque point sera construit selon l'axe vertical en lui assignant la valeur Z'=Z+hauteur_attributaire. Une fois ces points connus, nous pouvons construire nos murs selon un découpage en triangle. On utilise des triangles car la partie 3D est gérée par la librairie OpenGl, qui est très peu gourmande en mémoire si l'on découpe la scène 3D en triangles. À ce niveau de développement, des toits ont été ajoutés sur les bâtiments ayant 4 cotés, de façon automatique (c). Une fois ce découpage fait, un texturage est réalisé afin de couvrir les murs (d). Comme pour les murs, une texture aléatoire est appliquée sur les toits.
Cas des données linéaires: exemple des routes
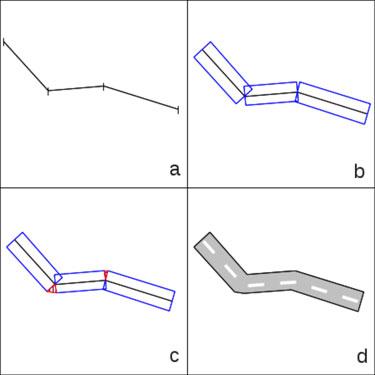
| 2. Dessin des routes 3D à partir d'un chevelu routier linéaire |
Les routes sont généralement décrites en tant que lignes, polylignes ou polygones. Nous allons nous intéresser aux lignes car la données OSM (Open Street Map, donnée accessible gratuitement sur internet) défini les routes de cette façon. Nous allons utiliser un attribut de cette donnée SIG pour transformer cette donnée 1D en 2D, puis avec l'ajout de la topographie nous allons obtenir une donnée 3D. Le schéma ci-contre explique le principe. Tout comme les bâtiments, nous allons utiliser les coordonnées définissant nos lignes (a). Pour chaque ligne, un attribut largeur est généralement présent. Si ce n'est pas le cas nous prenons une donnée par défaut. De la même manière, si une donnée existe concernant le type de voie (1x 2 voies, 2x 2 voies, …), nous l'utiliserons pour mieux créer notre rendu visuel. Cette largeur est utilisée pour obtenir un rectangle à plat ayant la même longueur que la ligne initiale et la largeur égale à la valeur attributaire (b). Pour chacun de ces points nous attribuons la valeur de la topographie sous-jacente pour avoir un objet 3D à représenter dans notre visualisation. Sur la figure b on peut observer des trous au niveau des bords de notre route. En effet, dans les virages, l'angle extérieur entre chaque segment n'est pas couvert par nos «rectangles de route». Pour cela nous allons remplir ces manques par des triangles rejoignant chacun des points (c). Pour arriver à cela un chevelu du réseau routier se doit d'être réalisé préalablement pour connaître la continuité des tracés. Nous aurons ainsi une numérotation des segments de route et donc le moyen de connaître l'emplacement de chacun de ces triangles. Ensuite un principe de texturage sera réalisé sur l'ensemble des triangles et on utilisera le réseau linéaire initial pour dessiner la limite entre les deux voies pour les parties à double sens (d). Ce processus de zone tampon (création d'une zone autour d'un objet selon une valeur de largeur) sera utile pour le passage de voiture sur la chaussée.
Outils dédiés à la visualisation
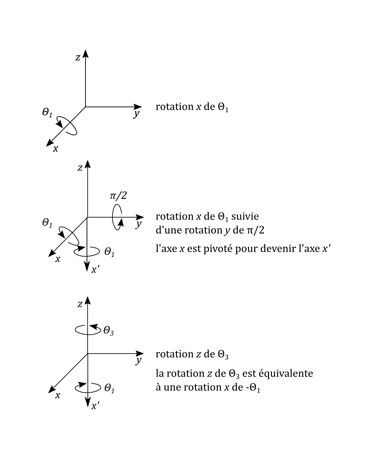
3. Phénomène du Gimbal Lock. Lorsqu'une rotation de 90° est exercée sur un axe, une superposition de 2 axes se produit et ainsi on perd un degré de liberté dans les rotations (Watt A., Watt M., 1992) |
Caméra et mouvements
La scène 3D générée n'est pas statique. Nous ne souhaitons pas que l'utilisateur soit juste un spectateur. Il peut à tout moment changer de point de vue sur la scène via un accès souris et/ou clavier. La souris permet de faire une rotation de la caméra tandis que les touches directionnelles servent à avancer, reculer ou translater dans l'affichage 3D. Tous les mouvements de caméra sont gérés via des quaternions. Les quaternions sont souvent utilisés dans les jeux vidéos pour deux principales raisons. La première est que les quaternions ne sont définis que par 4 nombres rééls (q=w+ix+jy+kz avec w définissant la partie scalaire et ix, jy, iz la partie vectorielle (Hamilton W.R., Hamilton W.E., 1866)) contrairement à une matrice de rotation qui est définie par 9 nombres réels. Lorsque la caméra n'est pas en mouvement, la différence n'est pas grande, mais lorsque l'on fait une rotation l'écart de temps entre les deux méthodes s'agrandit. En effet, lors d'une rotation, on multiplie les deux positions initiale et finale pour créer le mouvement. Pour une matrice de rotation 3x3, on va générer 81 calculs alors qu'avec les quaternions nous n'allons avoir que 16 calculs à effectuer.
La deuxième raison est que l'on évite le problème de gimbal locking (figure 3). Ce problème arrive lorsqu'une rotation de π/2 est exercée sur un axe. Une fois superposés, seulement 2 axes peuvent tourner tandis que le troisième reste figé. On appelle cela une perte de degré de liberté (Watt A., Watt M., 1992). Cela se produit si on utilise les angles d'Euler pour les rotations (ou alors les matrices de rotations qui ne sont, ni plus ni moins, que des utilisations plus détaillées des angles d'Euler).
Stéréoscopie 3D
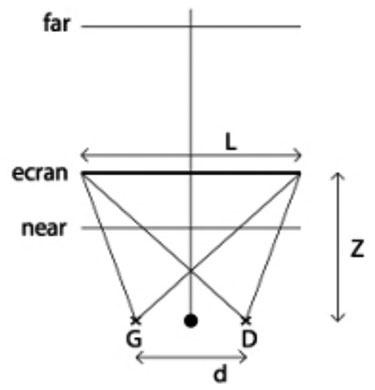
Le rendu 3D peut être accentué par la 3D stéréoscopique. Ce procédé, largement utilisé dans les films actuellement projetés au cinéma, consiste à tromper notre cerveau en décalant la scène affichée avec un point de fuite pour créer une perspective. Pour les films ayant une post-production 3D, c'est-à-dire n'ayant pas été tournés avec une caméra 3D, une technique de découpage par plan est réalisée. Le point de fuite ne sera pas le même selon le plan afin de rapprocher celui-ci de l'œil du spectateur. Ce procédé est illustré dans la figure 4. Nous utilisons ce même procédé avec l'emploi de la couleur. On appelle cela la stéréoscopie anaglyphique avec l'image gauche colorée en rouge et l'image droite colorée en cyan. Le fait de voir en volume le rendu de la ville générée en 3D permet à l'utilisateur de s'immerger dans la simulation. Cependant ce type de stéréoscopie possède une limite contraignante pour la modélisation en couleur.
4. Principe de la stéréoscopie. Un point de fuite est choisi ainsi qu'un décalage entre les deux images. En ajustant ce décalage, les objets seront interprétés en volume par notre cerveau de manière automatique. |
Le fait d'utiliser des lunettes bicolores pour afficher le relief rend la scène majoritairement grisâtre lors de la vision. Dans un futur proche nous allons appliquer la stéréoscopie de Holmes (Wendel, 1859) pour ne plus avoir cette perte de la coloration de la scène. Ce procédé inventé en 1859 est utilisé pour visualiser les vues aériennes et utilise des systèmes de lentilles ou de prismes pour la mise en relief. Les couleurs sont ainsi préservées.
Conlusion
Les SIG sont de plus en plus populaires grâce à la présence croissante d'Internet dans nos foyers ou nos déplacements. Nous les utilisons sans nous en rendre compte à longueur de journée avec les GPS, les cartes interactives, les jeux vidéos, les plans sur écrans tactiles dans les grandes surfaces, etc. La donnée géographique est aussi de plus en plus accessible et compréhensible grâce à Open Street Map qui permet à tous de créer de la donnée ou de l'utiliser. Le but de ce travail de thèse est d'apporter un outil se basant sur le fait que l'on peut utiliser de la donnée SIG standard pour modéliser des villes virtuelles en 3D et utiliser ces mêmes données pour simuler des phénomènes tels que le trafic routier. L'utilisation de ce logiciel se doit d'être accessible à tous et de privilégier l'interaction avec l'utilisateur. Pour arriver à cela, de nombreux algorithmes de conversion de la donnée ont été créés afin d'automatiser tous ces processus, eux mêmes cachés à l'utilisateur néophyte. Ce travail est encore en cours de développement.
Bibliographie
KENNEDY K., SQUIVIDANT H. (2004). Data in three dimensions: a guide to ArcGis 3D analyst. 256 p. ISBN: 978-1-401-84886-6
WATT A., WATT M. (1992). Advanced animation and rendering techniques: Theory and practice. États-Unis d'Amérique: Addison-Wesley Professional, 455 p. ISBN: 0-201-54412-1
HAMILTON W.R., HAMILTON W.E. (1866). Elements of quaternions. London: Longmans, 762 p. [PDF]
WENDEL H.O. (1859). The stereoscope and the stereograph. États-Unis d'Amérique: New Haven, Conn.: Leete's Island Books, 300 p.