Comment mesurer les déplacements dans l’Antiquité? L’illusoire précision du site Orbis
Le site de cartographie des transports dans l’Antiquité romaine Orbis, dont il a été rendu compte dans un récent numéro de Mappemonde (n°106, 2012), fournit un outil de modélisation remarquable par sa conception et par sa simplicité d’utilisation. Doté d’une interface inspirée des outils de navigation qui nous permettent de planifier nos déplacements actuels, il permet de proposer des itinéraires, des temps et des coûts de transport affinés en fonction de différents paramètres réglables. Si ce type d’outil présente un avantage évident en termes d’appréhension globale de la contrainte que constitue l’immensité de l’Empire romain, Denis Eckert et Frédérique Bertoncello, dans leur compte rendu, ont également souligné quelques limites du modèle, en particulier l’absence de la prise en compte de l’évolution des situations sur plusieurs siècles.
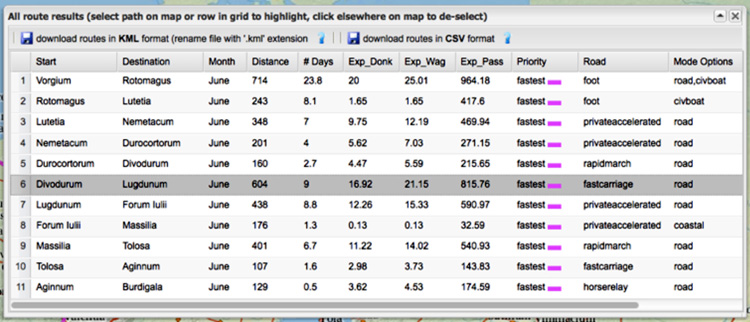
Cette courte note a pour objectif d’évoquer une question qui dépasse le seul cadre d’Orbis, mais qui est très importante dans cet outil cartographique: la précision des données. Lorsque l’on formule une requête dans Orbis, la réponse obtenue est une réponse exacte qui découle d’un calcul de moyenne. Tout en tenant compte des aléas climatiques ou de divers impondérables, elle génère un résultat sous une forme finie (fig. 1).
| 1. Un tableau de distances et de temps de transports généré par Orbis |
| Source: Orbis. Exemple tiré de Bertoncello, Eckert (2012) |
Or plusieurs indices laissent penser que, aussi bien durant l’Antiquité que le Moyen Âge, la prise en compte des coûts et des temps de transport devait plutôt se traduire par des fourchettes que par des valeurs absolues. La table de Peutinger (Peutingeriana Tabula Itineraria), une des sources fondamentales ayant servi à la construction de l’outil Orbis pour sa partie terrestre, contient en son sein les indices de cette relative imprécision. Cet «itinéraire» est une copie médiévale d’un document sans doute mis en forme au IVe siècle. Il donne un grand nombre de mesures de distance entre des villes, mais aussi des stations routières secondaires dont certaines sont difficiles à identifier. Les distances fournies ont d’ailleurs parfois servi à justifier la localisation de tel ou tel site [1]. L’édition de Talbert (2010) permet de disposer de l’ensemble de ces distances. Pour essayer de mieux comprendre la réalité des données métriques de ce document, j’ai rassemblé les informations de l’espace gaulois au sens large.
| 2. Valeurs de distance exprimées dans la table de Peutinger |
La compilation de l’ensemble de ces données fournit un corpus de 849 mesures avec une très grande variété de distances allant de 2 à 54 lieues. La moyenne de ces distances est de 15,6 lieues et n’est guère éloignée de la distance moyenne d’une étape journalière. La répartition spatiale des villes et vicus cités est par essence aléatoire. La distribution cumulative des mesures devrait suivre une loi normale, avec une courbe «en cloche», avec très peu de distances faibles et très peu de grandes distances. C'est de fait ce que montre la représentation graphique de ces données (fig. 2).
A priori, nous disposons donc de distances réalistes qui sont fournies avec une apparente précision; nous ne sommes pas loin d’Orbis. Cette apparence est cependant trompeuse. S’il est logique que la courbe ne soit pas complètement lisse, on doit constater qu’il existe de très nombreuses irrégularités. Ainsi alors que la carte ne fournit que 24 mesures de 11 lieues, elle en donne 87 de 12 lieues, mais seulement 26 de 13 lieues. Les irrégularités ne sont pas aléatoires. Plusieurs pics s’intègrent parfaitement dans un système comptable de base 12, système dominant. Il s’agit du nombre de mesures pour 3, 6, 12 et 16 lieues. Au-delà les pics répondent plutôt à une logique de base 5, avec des modes notables dans la distribution à 20, 25, 30 et 40 lieues. Il n’existe aucune raison pour que les distances entre villes se placent dans cette grille. Malgré les apparences, il est très vraisemblable que les distances données dans la table de Peutinger soient des distances approximatives. Mais quelle est la marge d’erreur, au-delà de celle due à l’absence de sous-multiples de la lieue?
À partir du tableau de données, il est possible de calculer la courbe de tendance polynominale d’ordre 4 correspondant à un lissage théorique des données en se limitant aux données comprises entre 0 et 26 lieues, de manière à ne pas prendre en compte les valeurs très hétérogènes au-delà de 26 lieues. La fonction obtenue est:
y = 0,0014x4 - 0,0661x3 + 0,6684x2 + 3,4635x - 2,718
L’écart moyen des données réelles par rapport à la donnée théorique est de 9,44. Mais on observe une répartition très inégale de ces données. 16 d’entre elles sont inférieures à la mesure théorique mais seulement 10 se situent au-dessus. Il n’est donc pas étonnant que parmi ces dix l’on observe les plus gros écarts à la courbe théorique. Pour essayer de mesurer la marge d’erreur, on lisse chaque écart avec les écarts des distances immédiatement supérieures et inférieures. On constate que l’écart moyen à la donnée théorique tombe alors à moins de 3,5 ce qui démontre que les écarts à la courbe théorique d’une mesure sont compensés par ceux, inverses, des mesures immédiatement supérieures et inférieures. Ce constat est vrai dès les courtes distances, mais s’accentue fortement au-delà de 10 lieues. Entre 1 et 10 lieues, l’écart à la courbe théorique est en moyenne de 4,34. Il est de 12,8 pour les distances comprises entre 10 et 25 lieues.
On peut donc conclure que la marge d’erreur des mesures fournies dans la table de Peutinger est de plus ou moins une lieue pour les distances comprises entre 0 et 10 lieues (soit au minimum 20% de marge), et qu’elle tend sans doute vers plus ou moins deux lieues lorsque la mesure atteint 25 lieues. Au-delà l’approximation devient très forte. La quasi-absence de mesures entre 35 et 40 lieues laisse penser que la marge d’erreur est alors au moins égale à plus ou moins 2,5 lieues. Ce type d’expression d’une réalité arrondie est rarement vérifiable sur des données sérielles antiques. Elle est très classique et presque une constante des systèmes de mesures du Moyen Âge (Portet, 2006).
Par ailleurs, un second élément d’ordre archéologique pousse également à relativiser la précision de l’espace et du temps que pouvaient avoir les Romains. L’archéologie préventive a, en France, permis de multiplier les découvertes de voies antiques. Si certaines peuvent être identifiées clairement au système des routes connues par les itinéraires et repris par Orbis, d’autres font partie d’un vaste maillage qui irrigue un espace déjà très fortement anthropisé dès la protohistoire. Or les données archéologiques montrent qu’en termes techniques, il n’est pas toujours facile de distinguer une voie majeure comme la Via Domitia d’une voie qui pourrait être considérée comme secondaire du seul fait qu’elle n’apparaît pas dans les itinéraires antiques (Vaginay, 2003). Cette absence de forte hiérarchisation technique des axes de déplacement pouvait se traduire par des axes routiers caractérisés plus par des faisceaux de chemins que par un unique axe concentrant tout le trafic (Kasprzyk, Nouvel, 2011). Cette segmentation des axes de circulation est encore la règle au Moyen Âge, en dehors des zones trop contraintes par le relief (Lartigaut, 1964) et ne disparaîtra réellement qu’avec la construction des routes royales au XVIIIe siècle.
Ces deux arguments me semblent montrer que, si les temps et les coûts de transport peuvent être estimés, on peut se demander s’il ne serait pas plus pertinent de fournir non pas un chiffre rond mais une fourchette de durée et de coût qui refléterait non seulement l’incertitude que pouvaient avoir les Gallo-Romains de leur temps de transport mais aussi la variété des axes routiers empruntables. L’intérêt serait alors de pouvoir mesurer le poids de cette incertitude (la largeur de la fourchette) et son impact économique éventuel. Il aurait été certainement possible d’intégrer dans Orbis un outil proposant des fourchettes de temps plutôt que des durées finies, en tenant compte de l’augmentation de la marge d’erreur en fonction des distances. Dans l’état actuel, Orbis a l’inconvénient de proposer au néophyte une précision dénuée de sens.
Bibliographie
BERTONCELLO F., ECKERT D. (2012). «Voyager dans l’Empire romain ou le Tour de Gaule en 80 jours», M@ppemonde, n°106
KASPRZYK M., NOUVEL P. (2011). «Les mutations du réseau routier de la période laténienne au début de la période impériale: apport des données archéologiques récentes». In REDDÉ M., BARRAL Ph., FAVORY Fr. Aspects de la romanisation dans l’Est de la Gaule. Glux-en-Glenne: Centre archéologique européen, coll. «Bibracte», n° 21, 966 p. ISBN: 978-2-9096-6868-0
LARTIGAUT J. (1964). «Les chemins de Cahors vers le Sud-Ouest au XVe siècle». Bulletin de la Société des Études du Lot, 1964, t. LXXXV, p. 13-32.
PORTET P. (2006). «La notion de précision dans la mesure médiévale». In RIGAUDIÈRE A., De l’estime au cadastre en Europe, Le Moyen Âge, actes du colloque de Bercy des 11-13 juin 2003. Paris: Comité pour l'histoire économique et financière de la France, p. 151-160. ISBN: 2-11-094-789-6
TALBERT R.J.A. (2010). Rome’s World: The Peutinger map reconsidered. Cambridge, New York, Melbourne: Cambridge University Press, 376 p. ISBN: 978-0-5217-6480-3 (consulter)
VAGINAY M. (2003). Histoire des sites, histoire des hommes : découvertes archéologiques réalisées lors de la construction de l’autoroute A20 en Quercy. Rodez: Éd. du Rouergue, 236 p. ISBN: 2-84156-464-9